The Stomachion |
||
|
Introduction |
There's a puzzle that survives since the time of Archimedes (287 B.C. - 212 B.C.) that merits a look. It is also called the Loculus of Archimedes, because Archimedes studied and wrote about it, although it is unclear whether he invented it or not. It is a square divided into fourteen pieces. It is deceptively difficult, although there are many alternate solutions. It now appears that in speculating about how many different solutions there might be to this puzzle, Archimedes anticipated the branch of mathematics called combinatorics. In October of 2003,
Bill Cutler
used a computer program to enumerate them. Barring rotations, reflections,
and the permutation of identical pieces, there are 536 distinct solutions. See
this link for more information on Bill's solution. On the other hand,
you might want to see how many of them you can find on your own!
Here is another view of Bill's work. |
|
|
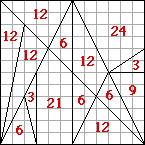
The arrangement below is the "canonical" solution, the one you almost always see in the literature. Each piece's relative area is indicated. The total area is 144 units and each of the pieces is commensurate with the area of the square. For example, the piece with area "21" represents 7/48 of the total area.
Diagram courtesy Chris Rorres, University of Pennsylvania In addition to reassembling the square from the pieces, the Greeks also tried to form various figures using all the pieces, much as we do with tangrams today. Although this puzzle was much remarked upon by the ancients, it seems to have been ignored in modern times. For more information, see this article by Professor Chris Rorres. There is also a wealth of information on Archimedes available. Some more very original research on the puzzle can be found here. |
The Puzzle |
|
|
Archimedes and Kadon |
Our friends at Kadon Enterprises announced commercial availability of this ancient puzzle in August, 2003. See this link for more details. I am very happy to have brought this puzzle to their attention; together, we are reviving a 2,250 year-old gem. To Kate Jones of Kadon goes the credit for having the perspicacity to appreciate the historical significance of this puzzle, and the gumption to bring it to the public in a beautiful form at a reasonable price. ~~~ Chronology ~~~ April 2003: Joe Marasco contacts Kate Jones of Kadon to produce the Stomachion prototype; Kate's first reaction: "Is there more than one solution to the puzzle?" May 2003: First prototypes available; Marasco discovers the Palimpsest/Reviel Netz connection. August 2003: Jones announces general availability of the puzzle from Kadon at the annual International Puzzle Party in Chicago. September 2003: Prototype received as a gift by Netz from Marasco. October 1, 2003: Marasco and Netz meet at Stanford and discuss the Stomachion; they wonder if Archimedes had considered how many distinct solutions there are, as it is now clear that there are many. October 2003: Marasco posts $100 bounty for first correct answer to "number of solutions"; sets time limit of November 15; erroneously "guesses" 537 solutions; Jones forwards Marasco's challenge to Bill Cutler, Ed Pegg Jr, and others. October 31, 2003: Cutler wins the bounty with his correct answer of 536 solutions; see below for more details. November 2003: Pegg publishes Cutler's answer; Fan Chun and Ron Graham announce graph theory/combinatoric answer of 17,152 solutions, which is equivalent to Cutler's; Persi Diaconis and Susan Holmes also contributed to this result. December 2003: Netz presents his conclusion at Princeton – Archimedes indeed considered the combinatoric implications of the Stomachion, and was the first to pioneer that branch of mathematics. December 14, 2003: Front page story by Gina Kolata in the Sunday New York Times, in which the "more impressive" Chun-Graham answer of 17,152 is promulgated; confusion at first as they did not reduce for rotational and reflection symmetries and permutation of identical pieces; the article claims that Cutler "confirmed" the Chun-Graham result, but in fact it was the other way around, as Chun and Graham admit on their web site and Netz confirms in his book (see below). |
|
|
One should also see the link to the Palimpsest. This recently recovered document contains the oldest reference to the Stomachion, as well as containing other priceless texts concerning the discoveries of Archimedes. Professor Reviel Netz of Stanford is currently working on elucidating the Palimpsest, and he has a particular interest in the Stomachion. Here is a photo of him with one of the Kadon Enterprises Stomachion prototypes, originally sent to him by yours truly. Note that the pieces are arranged differently than in the "canonical" solution shown above. It was this very discrepancy that led Reviel to discover that there was more than one solution – his "Aha!" moment.
PHOTO: NY TIMES This photo is from the December 2003 article in The New York Times. I am the "retired businessman from California" mentioned therein. For more details, click here. See also the work of Fan Chung and Ron Graham, who were brought into the fray by Persi Diaconis and Susan Holmes. Dr. Netz has recently (2007) published a book
with William Noel, the Curator of Manuscripts at The Walters Art Museum,
Baltimore, and the Director of the Archimedes Palimpsest Project. The book is
called
The Archimedes Codex. Chapter 10 tells the story we describe above from
Reviel's personal perspective. See also this article in Stanford Magazine. Note the picture therein with the same Kadon prototype; in this photograph, the pieces are arranged in the "canonical" solution, probably because this was a more "posed" picture than the New York Times photo above. |
The Palimpsest |
|
|
Bill Cutler's Bounty |
I was so interested in getting an answer to the Stomachion that I resorted to old-fashioned capitalism: I posted a "bounty" for the solution to my programmer friends. Here is the exact text of the e-mail message I sent them. Kate Jones passed it on to Bill Cutler, who was already working on the problem at her request. There is this geometrical puzzle called the Stomachion that dates from the time of Archimedes. Here is the puzzle: The numbers just refer to the area of each piece relative to the total area of 144 units. For more details, see: http://www.barbecuejoe.com/stomachion.htm and http://www.gamepuzzles.com/archsqu.htm. It would appear that there is an interesting UNSOLVED problem relative to this puzzle. How many unique solutions are there? Clearly, there are many. To start with, note the left and right symmetry caused by the vertical line going down the middle. Further, note that there are essentially four right triangles, each composed of either three or four pieces, that make up the solution (for example, the pieces marked 24, 3, and 9 make up one of them; the two 12's and two 6's make up another.) There are some "counting" issues. For example, note that there are two 12's that are identical, so merely interchanging them should not constitute a "different" solution, unless you want to define it so. Also to be considered is the issue of turning the puzzle over, as well as taking any solution such as this one and creating three "new" ones by successive 90 degree rotations around one corner. I leave it up to you to define what constitutes a "unique solution." Pick your own rules, and state them clearly. Then write a program that tells us how many solutions there are. Should be simple enough. I have it on good authority that this problem remains UNSOLVED and that it is at least 2200 years old. If you find a solution, I can get you credit in a forthcoming paper by professor Reviel Netz of Stanford, a classics professor who is writing on the subject of the Stomachion and would like to know the answer. It's not exactly Fermat's Last Theorem, but it's a worthy problem. And I think it is non-trivial, although do-able by the right group of people. To sweeten the pot, I will offer a BOUNTY of $100 for a solution before midnight November 15, 2003. To qualify for the bounty, you must be willing to demonstrate the program and defend your solution. Any takers? Clarification on the bounty: I will pay one (1) prize of $100 to the first correct solution received before midnight November 15, 2003. No multiple awards, and no awards for incorrect solutions. If you just give me a number, such as "537," then you will have to wait for either confirmation or refutation to earn (or not earn) the reward. If you can convince me that the solution must be correct, the award will be accelerated accordingly. The bounty can of course be awarded to a team of solvers, to be shared as they see fit. I want to reward solution finders, not language lawyers or loophole finders. Decisions of the judges will be final. Bill Cutler won the bounty with his correct answer of 536 solutions on October 31, 2003. He was the only programmer to submit a solution. |
|